kdeedu, kde)



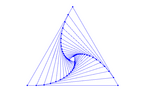
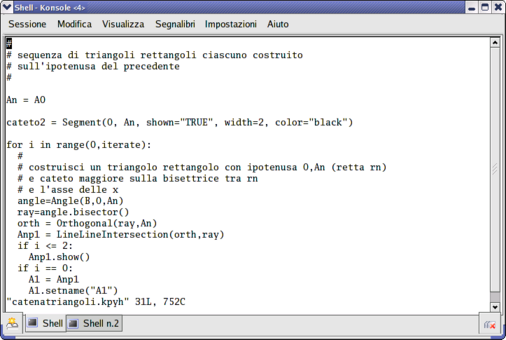
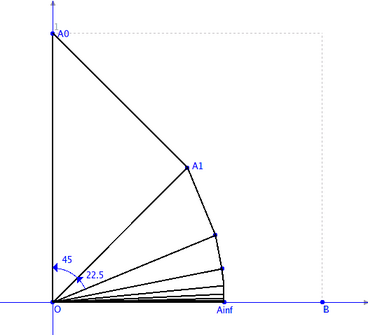 Partiamo dal triangolo rettangolo T0 di vertici (0,0), (0,1),
(1,1).
Vogliamo costruire una sequenza infinita di triangoli rettangoli
T0,
T1,
T2, ... aventi angolo nell'origine di valore rispettivamente
45o,
45o/2,
45o/4, ...
Ognuno ha l'ipotenusa su un cateto del precedente, come illustrato
nella figura.
I vertici sulle ipotenuse, opposti all'origine, sono indicati con
A0,
A1,
A2, ...
Partiamo dal triangolo rettangolo T0 di vertici (0,0), (0,1),
(1,1).
Vogliamo costruire una sequenza infinita di triangoli rettangoli
T0,
T1,
T2, ... aventi angolo nell'origine di valore rispettivamente
45o,
45o/2,
45o/4, ...
Ognuno ha l'ipotenusa su un cateto del precedente, come illustrato
nella figura.
I vertici sulle ipotenuse, opposti all'origine, sono indicati con
A0,
A1,
A2, ...
Chiaramente i punti An convergono verso un punto sull'asse delle ascisse Ainf.
Si chiede:
kig

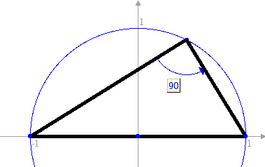
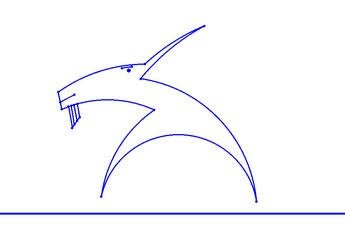
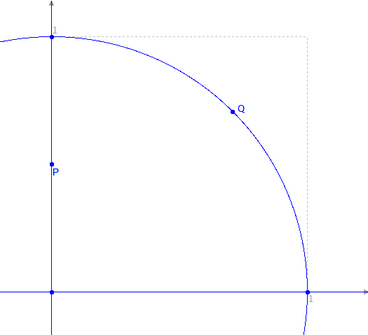 Il punto P si muove con velocità costante sul segmento
OA, mentre Q si muove con velocità costante sull'arco
del cerchio unitario nel primo quadrante.
La retta orizzontale per P e la retta per l'origine passante per Q
si intersecano in un punto che descrive la curva quadratrice
di Ippia
Il punto P si muove con velocità costante sul segmento
OA, mentre Q si muove con velocità costante sull'arco
del cerchio unitario nel primo quadrante.
La retta orizzontale per P e la retta per l'origine passante per Q
si intersecano in un punto che descrive la curva quadratrice
di Ippia