Tassellazioni periodiche / disegni periodici
Esistono almeno due traslazioni in direzioni
diverse che lasciano il risultato invariato.
Per traslazione si intende uno spostamento rigido
del piano parallelamente a sè stesso, ovvero
senza rotazioni nè riflessioni.
Ma, come abbiamo visto, ci possono essere anche simmetrie
di altro tipo nascoste nel disegno.
Le traslazioni sono casi particolari di isometrie,
ovvero trasformazioni che lasciano invariate le distanze:
movimenti rigidi. Abbiamo:

- rotazioni (di un certo angolo attorno ad un certo punto)
- riflessioni (rispetto ad una certa retta)
- traslazioni (già menzionate)
- glissosimmetrie:
combinazione di una riflessione ed una traslazione

Un esempio, anzi: tre
- Una disposizione a spina di pesce (il pavimento
nella zona bassa della fotografia) [pgg,22x]
- Una disposizione che ricorda un muro di mattoni
(il pavimento nella zona sotto all'estintore) [cmm,2*22]
- Una disposizione a quadretti (il soffitto) [p4m,*442]
Esercizio: riconosciamo le (due) simmetrie di
traslazione
Ci sono però anche altre simmetrie, più
o meno nascoste:
- simmetrie di riflessione sono chiaramente presenti
nel caso 2 e 3
- rotazioni di 90 gradi si possono fare nel soffitto
(caso 3)
- rotazioni di 180 gradi si possono fare nel caso 2
- Nel caso 1 è presente una glissosimmetria
Identificare, riconoscere, classificare!
Disegni diversi possono condividere le stesse simmetrie
L'autore de Il disordine perfetto (Marcus
du Sautoy) visita l'Alhambra con la famiglia e si imbatte
in due diversi motivi periodici:
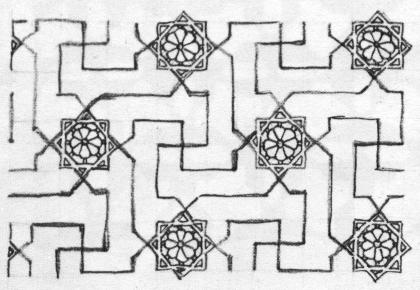 "La figura [3.3] mostra le mattonelle sulla prima parete
che accoglie i visitatori all'ingresso dell'edificio"
"La figura [3.3] mostra le mattonelle sulla prima parete
che accoglie i visitatori all'ingresso dell'edificio"
 "[...] Sul soffitto compare un altro motivo molto amato
dagli artisti dell'Alhambra[...]"
"[...] Sul soffitto compare un altro motivo molto amato
dagli artisti dell'Alhambra[...]"
L'autore si domanda ora se i due disegni condividono le stesse
simmetrie... la risposta passa da sì a no
ripetutamente man mano che si ragiona sulle figure.
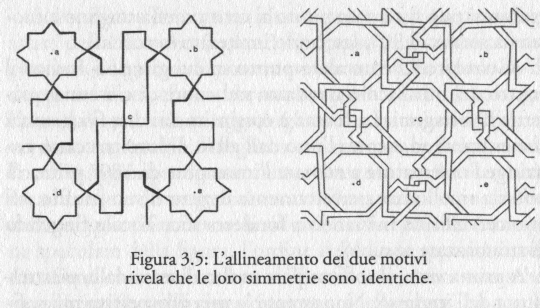 La risposta finale è sì, la corrispondenza
da fare tra i due disegni è illustrata in figura,
sicuramente piuttosto sorprendente. [p4,442]
La risposta finale è sì, la corrispondenza
da fare tra i due disegni è illustrata in figura,
sicuramente piuttosto sorprendente. [p4,442]
Le domande che sorgono spontanee a questo punto sono:
- come fare a riconoscere
se due disegni hanno le stesse simmetrie?
- quante diverse strutture possono esserci?
La Teoria dei Gruppi
Le isometrie del piano formano un gruppo:
- Se compongo due isometrie, ovvero se eseguo prima
una isometria e poi l'altra, ottengo ancora una isometria
- L'operazione contraria di una isometria (cioè il
movimento fatto alla rovescia) è a sua volta una isometria
- Vale la proprietà associativa: se A, B,
C sono tre isometrie si ha
(AB)C = A(BC)
(spiegare!)
- C'è una particolarissima isometria, che lascia tutto
fermo, che chiameremo identità
Nota: Non vale invece (in generale) la proprietà
commutativa!
Quelle particolari isometrie che risultano essere simmetrie
del disegno formano a loro volta un gruppo, sottogruppo
del gruppo di tutte le isometrie.
Si tratta di un gruppo infinito, poiché (ad esempio)
ci sono infinite traslazioni generate da due di esse.
In ogni caso il linguaggio matematico della teoria dei gruppi
è perfettamente adatto per il nostro scopo di
classificazione.
Risultato:
Ci sono esattamente 17 diversi gruppi di simmetria possibili
per una tassellatura periodica (o un disegno periodico)!
Corrispondenza tra class. di Conway e quella cristallografica
| Conway |
o |
xx |
*x |
** |
632 |
*632 |
| Cristal. |
p1 |
pg |
cm |
pm |
p6 |
p6m |
| Conway |
333 |
*333 |
3*3 |
442 |
*442 |
4*2 |
| Cristal. |
p3 |
p3m1 |
p31m |
p4 |
p4m |
p4g |
| Conway |
2222 |
22x |
22* |
*2222 |
2*22 |
|
| Cristal. |
p2 |
pgg |
pmg |
pmm |
cmm |
|
Come riconoscere il gruppo giusto
Si può utilizzare la seguente tabella (presa da
wikipedia inglese con chiave di ricerca wallpaper group):
Rotazione
minima |
Ci sono riflessioni? |
| Sì |
No |
| 360° / 6 |
p6m |
p6 |
| 360° / 4 |
| C'è un asse di rifl. a 45°? |
| Sì: p4m |
No: p4g |
|
p4 |
| 360° / 3 |
| C'è un centro di rot. non sugli assi? |
| Sì: p31m |
No: p3m1 |
|
p3 |
| 360° / 2 |
| Ci sono assi di rifl. perpendicolari? |
| Sì |
No |
| C'è un centro di rot. non sugli assi? |
pmg |
| Sì: cmm |
No: pmm |
|
| C'è una glissosimmetria? |
| Sì: pgg |
No: p2 |
|
| none |
| Glissosim. con asse non di rifl.? |
| Sì: cm |
No: pm |
|
| C'è una glissosimmetria? |
| Sì: pg |
No: p1 |
|
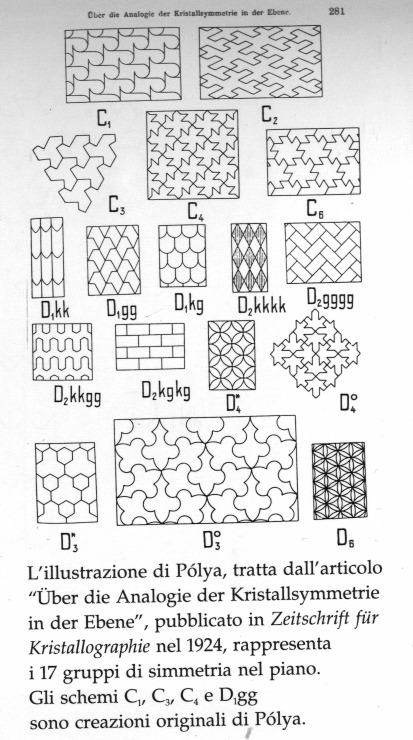 Ecco una classificazione dovuta a Pólya,
immagine tratta da Visioni della Simmetria
Ecco una classificazione dovuta a Pólya,
immagine tratta da Visioni della Simmetria
Prosegui: curiosità



 "La figura [3.3] mostra le mattonelle sulla prima parete
che accoglie i visitatori all'ingresso dell'edificio"
"La figura [3.3] mostra le mattonelle sulla prima parete
che accoglie i visitatori all'ingresso dell'edificio"
 "[...] Sul soffitto compare un altro motivo molto amato
dagli artisti dell'Alhambra[...]"
"[...] Sul soffitto compare un altro motivo molto amato
dagli artisti dell'Alhambra[...]"
 La risposta finale è sì, la corrispondenza
da fare tra i due disegni è illustrata in figura,
sicuramente piuttosto sorprendente. [p4,442]
La risposta finale è sì, la corrispondenza
da fare tra i due disegni è illustrata in figura,
sicuramente piuttosto sorprendente. [p4,442]
 Ecco una classificazione dovuta a Pólya,
immagine tratta da Visioni della Simmetria
Ecco una classificazione dovuta a Pólya,
immagine tratta da Visioni della Simmetria