
Il bello delle superfici minime, è che hanno un riscontro reale. Se uno costruisce un telaio di fil di ferro e lo immerge in acqua e sapone, sul telaio si formerà una pellicola. La superficie formata dalla pellicola è proprio una superficie minima che risolve il problema di Plateau.
Ora non voglio entrare nei dettagli, ma presentare subito una carrellata di superfici minime.
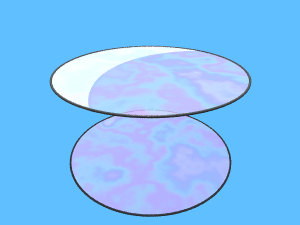
 Se ad esempio prendiamo come bordo due circonferenze, possiamo avere
due diversi minimi locali uno sconnesso e uno connesso: i due dischi
oppure la catenoide.
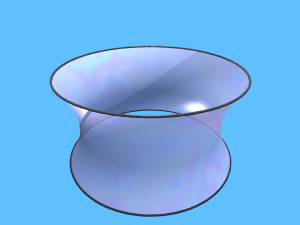
Se ad esempio prendiamo come bordo due circonferenze, possiamo avere
due diversi minimi locali uno sconnesso e uno connesso: i due dischi
oppure la catenoide.
Se prendiamo la seguente curva chiusa:


 possiamo ottenere come minimo locale per l'area sia una superficie
non orientabile (il nasto di Möbius) che una superficie orientabile.
Entrambe queste superfici sono regolari in tutti i punti.
possiamo ottenere come minimo locale per l'area sia una superficie
non orientabile (il nasto di Möbius) che una superficie orientabile.
Entrambe queste superfici sono regolari in tutti i punti.
Un primo esempio di superficie minima non regolare si ha prendendo il
seguente bordo:

La superficie di area minima in assoluto è una superficie con
una circonferenza di punti singolari (in tali punti si incontrano tre
superfici con un angolo di 120 gradi):
 ma otteniamo dei minimi relativi richiedendo che la superficie sia
regolare (ma non orientata):
ma otteniamo dei minimi relativi richiedendo che la superficie sia
regolare (ma non orientata):
 oppure orientabile:
oppure orientabile:

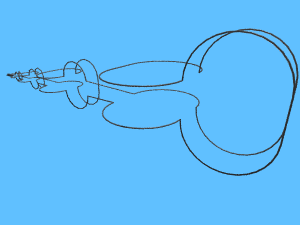
 Il seguente esempio mostra come si possano addirittura trovare superfici
minime di genere infinito. Il bordo di questa superficie è
ancora una curva chiusa continua.
Il seguente esempio mostra come si possano addirittura trovare superfici
minime di genere infinito. Il bordo di questa superficie è
ancora una curva chiusa continua.
Per esprimere matematicamente il problema di Plateau, è necessario dare una definizione rigorosa di superficie. Una possibilità è definire una superficie come l'immagine di una funzione continua da un certo dominio bidimensionale fissato nello spazio tridimensionale (superficie in forma parametrica).
 Ad esempio questa superficie minima (elica cilindrica) può essere
parametrizzata su un dominio di tipo disco.
Ad esempio questa superficie minima (elica cilindrica) può essere
parametrizzata su un dominio di tipo disco.

 Ad esempio queste due superfici hanno lo stesso bordo.
La superficie di sinistra è la superficie di area minima tra
tutte le superfici date in forma parametrica con dominio di base un disco.
Mentre a destra si trova la superficie minima che si realizza in
pratica come pellicola di sapone.
Si nota inoltre che la funzione che descrive la superficie in forma
parametrica non è iniettiva (c'è un'autointersezione)
mentre la "vera" superficie minima è del tutto regolare.
Ad esempio queste due superfici hanno lo stesso bordo.
La superficie di sinistra è la superficie di area minima tra
tutte le superfici date in forma parametrica con dominio di base un disco.
Mentre a destra si trova la superficie minima che si realizza in
pratica come pellicola di sapone.
Si nota inoltre che la funzione che descrive la superficie in forma
parametrica non è iniettiva (c'è un'autointersezione)
mentre la "vera" superficie minima è del tutto regolare.
 Questa ad esempio è la superficie che si ottiene prendendo come curva di
bordo gli spigoli di un cubo. La superficie così ottenuta
è interessante anche perché presenta entrambi i tipi di
singolarità possibili per le superfici minime (stiamo parlando
qui di superfici di dimensione 2 in uno spazio di dimensione 3).
Ci sono infatti dei punti (disposti lungo 12 "segmenti") della superficie in cui si incontrano tre
superfici con un angolo di 120 gradi e ci sono poi i quattro vertici
del "quadrato" centrale in cui si incontrano 4 superfici con un angolo
di circa 108 gradi.
Questa ad esempio è la superficie che si ottiene prendendo come curva di
bordo gli spigoli di un cubo. La superficie così ottenuta
è interessante anche perché presenta entrambi i tipi di
singolarità possibili per le superfici minime (stiamo parlando
qui di superfici di dimensione 2 in uno spazio di dimensione 3).
Ci sono infatti dei punti (disposti lungo 12 "segmenti") della superficie in cui si incontrano tre
superfici con un angolo di 120 gradi e ci sono poi i quattro vertici
del "quadrato" centrale in cui si incontrano 4 superfici con un angolo
di circa 108 gradi.
Quest'altro esempio è una superficie che si retrae sul proprio bordo.

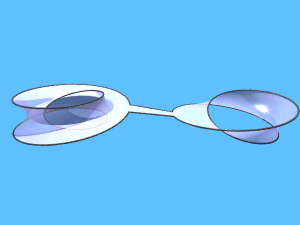 È possibile (sebbene non sia per niente intuitivo) deformare
questa superficie lasciando fisso il bordo fino a farla coincidere col
proprio bordo. Questo può far pensare che questa superficie in
qualche senso non sia un minimo assoluto per l'area, in quanto si
deforma in una superficie di area zero.
È possibile (sebbene non sia per niente intuitivo) deformare
questa superficie lasciando fisso il bordo fino a farla coincidere col
proprio bordo. Questo può far pensare che questa superficie in
qualche senso non sia un minimo assoluto per l'area, in quanto si
deforma in una superficie di area zero.


Quest'altra superficie è frutto più che altro di una
curiosità. Sapendo che data comunque una curva chiusa è
possibile trovare una superficie di area minima con bordo la curva
data, ci si chiede come può essere fatta una superficie che ha
come bordo una curva che si annoda.
In questo esempio viene mostrata la superficie minima che ha come
bordo il nodo trifoglio, che è il più semplice nodo non
banale.
 Come ultimo esempio vediamo come non sia ovvio capire quale sia la
superficie minima con un certo bordo. Se ad esempio si prende come
bordo l'unione di tre circonferenze disgiunte, la superficie minima
è quella che si può vedere in figura.
Questa è una superficie "omeomorfa" ad un disco con due buchi
ed un manico.
Come ultimo esempio vediamo come non sia ovvio capire quale sia la
superficie minima con un certo bordo. Se ad esempio si prende come
bordo l'unione di tre circonferenze disgiunte, la superficie minima
è quella che si può vedere in figura.
Questa è una superficie "omeomorfa" ad un disco con due buchi
ed un manico.