Problem: Find the equilibrium shape of a rope of length 2L which hangs from the two endpoints at x-coordinates x = -a and x = a. The endpoints are at the same height of y = 0 (notice that I have redefined the length of the rope to be 2L since the numbers will work out easier in the result).
Let M be the total mass of the rope, dm be a differential mass element of the rope, and ds be a differential linear segment of the rope. Then
![]()
Let dU be the differential potential energy of the differential linear segment of the rope. Then
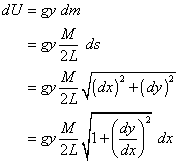
The total potential energy is given by
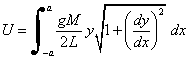
The rope is also subject to the constraint that its total length is 2L. Therefore
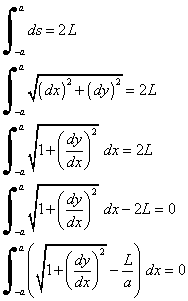
Thus, we must stationarize the function
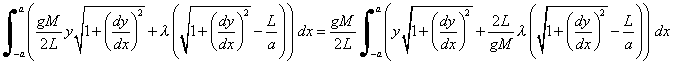
where l is a Lagrange undetermined multiplier. Let l' be a general
constant and![]() ; then the above function is given by
; then the above function is given by
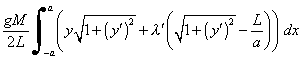
Recall that a function is stationarized in the Calculus of Variations if it obeys the Euler-Lagrange Differential Equation. Since the above function does not depend explicitly on x, the “Second Form” of the Euler Equation (Equation (5)) can be used.
Let ![]() and insert into Equation
(5). Therefore
and insert into Equation
(5). Therefore
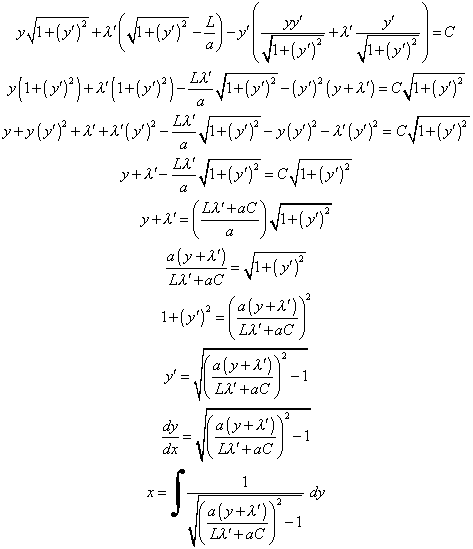
The constants in the above integral can be combined, and the integral is then written compactly as
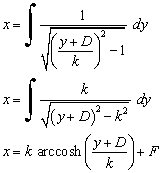
where k, D, and F are constants. Solving the above equation for y gives
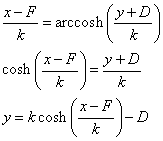
Therefore, the shape of the rope is a cosh function with constants which can be fitted to the initial conditions.
The conditions y(-a) = 0 and y(a) = 0 give
![]()
The above equations simultaneously hold when F = 0. Setting F = 0 and using the condition y(a) = 0 again gives
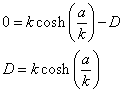
which gives the constant D as a function of a and k.
The condition that the rope’s total length is 2L gives
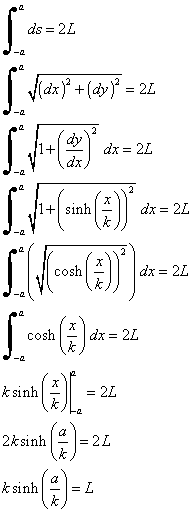
The above transcendental equation is solvable numerically and gives the constant k.