Symmetric octominoid configurations

• Table of octominoid configurations not in magic27 table
• Local copy of the Jürgen Köller [Ko] magic27 table [link]
• Snapshots of real puzzle constructions not in magic27 table
• Trivia and remarks
• Syntax of an octominoid description code
• Syntax of a Rubik's Magic configuration code
• references

• magic27_annotated.txt: Analysis of the table magic27 ordered by coordinates in the table
• POV-Ray images of some GRAY configurations (configurations with both vanishing invariants but not yet constructed by me with the puzzle). Update (2015/02/01): All those configurations have subsequently been constructed, right now there are no gray configurations.
• Complete list of 3D octominoid configurations of the Rubik's Magic that have both metric and topological vanishing invariants. Listed by rubiksmagic code.
• Source code and header file of the program computing the two invariants.

TABLE 1

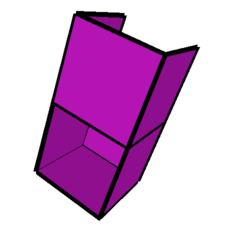
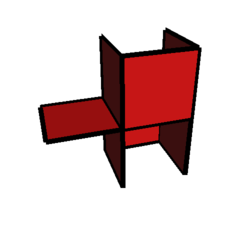
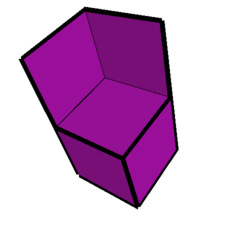
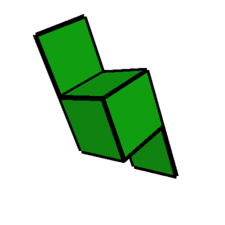
011-013-101-110-112-123-211-213s	011-013-101-112-123-211-213-312s	011-013-101-103-110-112-121-211s	011-013-103-105-112-114-123-213s
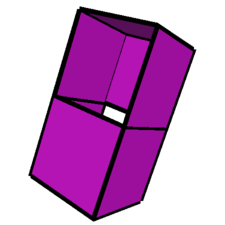
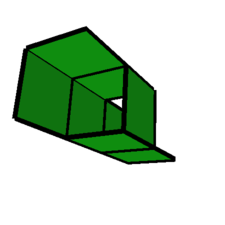
011-013-101-110-112-121-211-231s	011-013-031-123-132-134-143-233s	011-013-101-110-114-123-211-213s	011-013-015-101-103-123-125-213s
112-121-123-132-211-233-312-332s	112-121-123-211-213-231-323-332s

TABLE 2

TABLE 3

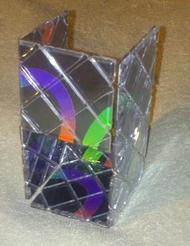
011-013-101-110-112-123-211-213s	011-013-101-112-123-211-213-312s	011-013-101-103-110-112-121-211s	011-013-103-105-112-114-123-213s
011-013-101-110-112-121-211-231s	011-013-031-123-132-134-143-233s	011-013-101-110-114-123-211-213s	011-013-015-101-103-123-125-213s
112-121-123-132-211-233-312-332s	112-121-123-211-213-231-323-332s

I only recently found the very interesting paper [Ver] where the topological invariant is also introduced.
• The armchair (first picture in tables 1 and 3) was the last feasible octominoid to be actually constructed.
  1. Start from the configuration of this image (instructions to get there can be found in [Pao])
  2. close both flaps (turning them 90 degrees)
  3. switch the hinging side of both flaps and open carefully (there is some stretching!)
  4. the resulting shape has a form almost identical to the cubechair (third picture in tables 1 and 3 above). It has two superposed tiles.
  5. turn 90 degrees one of the two superposed tiles (as a flap).
  6. another tile becomes a flap and can be turned down 180 degrees. We get to the cubechair shape above.
  7. push the same flap further inside the cube 90 degrees against the upper tile of the cube, which becomes a flap.
  8. Finally lift that new flap 90 degrees in the desired position.
• The cube (row 2, column 11 in table 2) can be realized by 3 distinct puzzle configurations, two are constructible: one (RmRmUmLmLmDvDmDv) is described in [Ko], the other (RmRmDmLmLvRmLvUm) can be reached from configuration of row 1, column 14 in table 2. The remaining configuration (RmRmUmLmLvRmLvDm) has both vanishing invariants, but I don't know if it is constructible.
• The basket (row 6, column 10 in table 2) has two distinct realizations with the puzzle, both constructible. One is described in [Ko] as an intermediate configuration towards the cube, the other is discussed in [Pao].
• The two cubes with flaps above: the first green (row 1, column 4 in table 1) and the second red (row 2, column 1 in table 1) can be constructed from the cube variant 2 (RmRmDmLmLvRmLvUm) by flipping a tile inside the cube.
• The third red configuration above (row 2, column 2 in table 1) has two realizations, both are constructible from the two realizations of the "basket" shape.
• The first light blue configuration of table 1 (row 3, column 1 in tables 1 and 3) can be obtained by starting from configuration in row 2 column 7 of table 2.

Each sequence of three integers xyz indicates the position of a square by means of the coordinates of its center. The only even coordinate indicates the orientation of the square.

The presence of the (optional) final 's' indicates that the given configuration corresponds to a symmetric octominoid (with respect to any isometry of space).

Two octominoids are considered equivalent if related by an isometry of space (reflections included), the printed configuration descriptions correspond to a canonical selection among all equivalent octominoids, based on a suitable total ordering. The software code can compute the canonical representative of a given configuration.

Each tile can be oriented by drawing an arrow on one of its faces parallel to a side as explained in [Pao]. A valid Rubik's Magic configuration admits a consistent orientation of the tiles (one tile is oriented in any way, then all the others uniquely inherit their orientation). As explained in [Pao] the tile orientation is inherited by reflecting the arrow drawn on an adjacent tile.

In the octominoid configurations, consecutive tiles form an angle with three possible values:

• Straight: the two tiles are coplanar
• Mountain fold: they form a 90 degrees angle of mountain type (origami terminology) with respect to the faces with the arrow
• Valley fold: they form a 90 degrees angle of valley type

For example the sequence RRRURRRU is the flat starting configuration of the puzzle.

A sequence can be prefixed by a \ if the starting tile is of backslash type (the type of a tile, slash or backslash, is decided once we chose its orientation and depends on the direction of the nylon strings). Two configurations are considered equivalent if they are the same up to choice of the first tile of the circular list, the traversal direction of circular list and the choice of orientation (slash and backslash tiles must be considered as distinct).

[Ko]

http://www.mathematische-basteleien.de/magics.htm

[Pao]

http://arxiv.org/abs/1401.3699