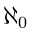 per indicare la cardinalità
del più piccolo insieme infinito: i numeri naturali N.
per indicare la cardinalità
del più piccolo insieme infinito: i numeri naturali N.

Se esiste una corrispondenza biunivoca tra due insiemi (finiti) è ovvio che questi hanno lo stesso numero di elementi (sono equipotenti).
Questo è il meccanismo scelto da Cantor per trattare gli insiemi infiniti: due insiemi (infiniti) hanno lo stesso numero di elementi (la stessa cardinalità) se si riesce a trovare una corrispondenza biunivoca tra di essi.
 L'insieme dei numeri naturali ha la stessa cardinalità
dell'insieme dei numeri pari... ma anche degli insiemi:
L'insieme dei numeri naturali ha la stessa cardinalità
dell'insieme dei numeri pari... ma anche degli insiemi:
In effetti si stabilisce che X ha meno elementi di 2X.
Ci sono quindi molti infiniti diversi: X, P(X), P(P(X)), ...;
Cantor ha quindi pensato di introdurre la notazione
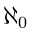 per indicare la cardinalità
del più piccolo insieme infinito: i numeri naturali N.
per indicare la cardinalità
del più piccolo insieme infinito: i numeri naturali N.
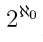 >
> 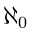 .
.
Prendiamo i numeri reali compresi tra 0 e 1; li possiamo scrivere in notazione posizionale (0,47687632...), ma usando la base 2 anziché la base 10, ad esempio 1/3 = 0,01010101...
Ora possiamo associare un sottoinsieme dei numeri naturali alla
sequenza di cifre dopo la virgola: se c'è un 1 il numero naturale
che corrisponde alla posizione nella sequenza appartiene all'insieme,
altrimenti non vi appartiene.
Ad esempio, 1/3 ha gli 1 nelle posizioni pari, quindi corrisponde
all'insieme dei numeri pari;
viceversa ad ogni sottoinsieme dei numeri naturali facciamo corrispondere
una sequenza di 0 e di 1 e quindi un numero reale tra 0 e 1.
Abbiamo trovato una corrispondenza biunivoca (quasi biunivoca, in realtà c'è un inghippo tecnico facilmente superabile) tra [0,1] e P(N)
Poi si dimostra che la cardinalità dell'intervallo [0,1] è la stessa di quella di tutti i numeri reali.
... che è la stessa dei punti del piano (!) e dei punti dello spazio (!!).


