Joseph Plateau

Fa vedere che le pellicole di sapone delimitate da un filo metallico ricurvo sono delle superfici minime.

Non è il caso delle bolle di sapone, ma questo è dovuto al fatto che una bolla racchiude un volume di aria isolato dall'esterno che determina una differenza di pressione tra l'interno e l'esterno della bolla. Se immaginiamo di introdurre una cannuccia, la bolla si sgonfierebbe...

Ecco un esempio del problema di Plateau

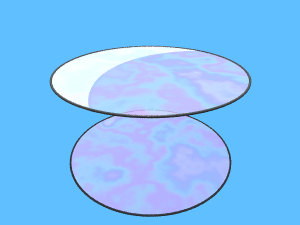
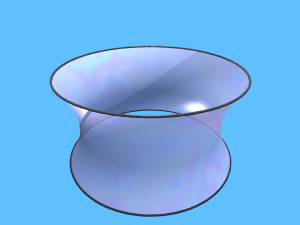
E qui ce ne sono molti altri costruiti da Emanuele Paolini (Univ. di Firenze)

Questo problema è stato inquadrato nell'ambito delle funzioni a variazione limitata dall'insigne matematico italiano Ennio de Giorgi.

Proprietà

Se la curva iniziale giace su un piano, ovviamente la superficie minima è anch'essa contenuta nel piano, e quindi il problema si banalizza
Non c'è unicità:

Notare che la seconda soluzione (che ricorda i vecchio box per bambini) altro non è che una catenaria fatta ruotare rispetto ad una retta verticale (catenoide)
Nei casi non banali la soluzione non è mai una superficie laterale di un cilindro o di una sfera, e non e' mai localmente convessa.
Forma di sella: in ogni punto la curvatura è positiva secondo certe direzioni e negativa secondo altre
Da un punto di vista teorico possiamo accettare superfici che si autointersecano:

Anche se in questi casi le soluzioni reali sarebbero probabilmente le seguenti:
Ci possono essere delle singolarità:
E possono essere anche piuttosto complesse:

Come affrontare il problema?

Intanto si tratta di un problema di ottimizzazione: la soluzione ha una superficie minima rispetto a tutte le altre superfici ammissibili. In effetti nella pellicola di sapone è nascosta una energia (tensione superficiale) che è direttamente proporzionale all'estensione della pellicola; siccome una pellicola di sapone è molto leggera, l'effetto della gravità può essere trascurato.

È possibile utilizzare il calcolo delle variazioni (equazione di Eulero-Lagrange, in una forma un po' diversa) per scoprire che una superficie minima ha sempre in ogni suo punto curvatura media nulla.

Cos'è la curvatura media?

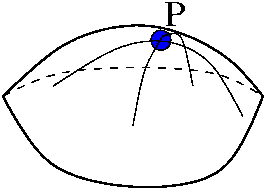Prendiamo un punto P su una superficie, e tracciamo una curva più dritta possibile sulla superficie che passi con una certa direzione v per il punto P; essa sarà comunque costretta ad incurvarsi a causa della forma della superficie.

Tale curvatura assume valori diversi a seconda della direzione v, ed avrà un valore massimo k_max e minimo k_min.

Nel caso di una superficie piana entrambi questi valori sono nulli, nel caso di una sfera sono uguali tra loro e dipendono dal raggio della sfera, per superfici generiche invece questi differiscono e possono anche avere segno diverso.

La curvatura media è la media aritmetica di questi due valori: (k_max + k_min)/2.

Dire quindi che una superficie ha curvatura media nulla equivale a dire che la curvatura massima è l'opposto della curvatura minima, in particolare la superficie si incurverà verso l'interno in certe direzioni e verso l'esterno in altre direzioni (come una sella).

Questa conoscenza non è purtroppo sufficiente per riuscire a fornire l'equazione esplicita di superfici minime se non in pochi casi particolari, ma permette comunque di derivare numerose proprietà interessanti. Una di esse si riferisce alla regolarità di una superficie minima; è stato per primo De Giorgi ad accorgersi che non è sempre vero che una superficie minima (sotto opportune condizioni) è regolare: ci può essere infatti una singolarità (un punto in cui la superficie non è bella liscia) se si tratta di una superficie in uno spazio di dimensione 8 (cono di Simons)!