ESPERIMENTO (mpeg)
ESPERIMENTO (mpeg)
Esperimento ideale:

dove "cosh" indica il coseno iperbolico:
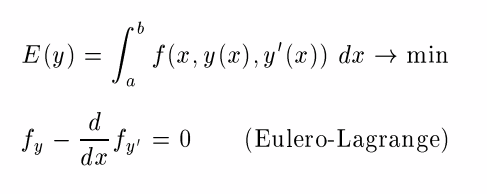
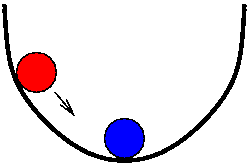 IDEA: La configurazione di equilibrio u di una pallina in
una scodella è quella di energia (potenziale) minima
E(u) = m g h(u).
Quindi trovare la soluzione equivale a ottimizzare
E(u)
IDEA: La configurazione di equilibrio u di una pallina in
una scodella è quella di energia (potenziale) minima
E(u) = m g h(u).
Quindi trovare la soluzione equivale a ottimizzare
E(u)
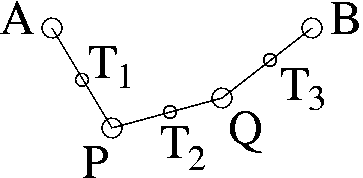 Una versione semplificata del problema della catenaria: cerco la
configurazione di equilibrio di un sistema di tre aste incernierate
con A e B fissati.
Una versione semplificata del problema della catenaria: cerco la
configurazione di equilibrio di un sistema di tre aste incernierate
con A e B fissati.
Voglio posizionare P e Q in modo che E(u) sia minima!
 Prendendo tante aste ottengo l'energia nel caso continuo
Prendendo tante aste ottengo l'energia nel caso continuo

C'è però da aggiungere il vincolo dell'inestensibilità |u'(s)| = 1 che rende la questione più complicata (ricerca di un minimo vincolato: equazione di Eulero-Lagrange + metodo dei moltiplicatori di Lagrange)